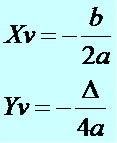funções

Noções iniciais de Função Quadrática

Toda expressão na forma y = ax² + bx + c ou f(x) = ax² + bx + c, onde os coeficientes a, b e c são números reais, sendo a ≠ 0, é considerada uma Função Quadrática(ou conhecida popularmente como equação do 2º grau), onde o valor y está em função do valor de x, isto é, x é considerado o domínio da função, enquanto y ou f(x) é a imagem.

Observe alguns exemplos de funções quadráticas:

y = 2x² + 6x + 10
f(x) = –6x² + 10x – 3
y = 7x² – 5x – 32
f(x) = 10x² – 6x
f(x) = x²
y = 14x² – 9
A função quadrática possui como representação geométrica uma parábola com concavidade voltada para cima ou para baixo de acordo com o valor do coeficiente a. Observe:

Raízes de uma função do 2º grau

As raízes de uma função quadrática são dadas quando fazemos y ou f (x) igual a zero, constituindo a função numa equação quadrática(ou popularmente equação do 2º grau).

Veja:
y = ax² + bx + c
y = 0
ax² + bx + c = 0
Podemos resolver uma equação do 2º grau utilizando o teorema de Bháskara:

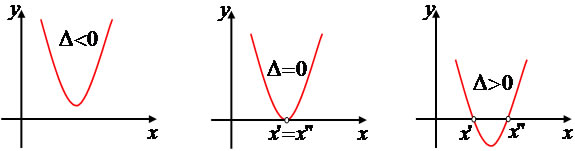
O resultado determina quantas raízes a função possui e em quantos pontos a parábola intersecciona o eixo x. Essa situação também pode ser dada de acordo com o valor do ∆ da equação quadrática. Observe as relações nos gráficos a seguir:

• ∆ < 0: não possui raízes reais, a parábola não possui ponto em comum com o eixo x.
• ∆ = 0: possui uma única raiz real, a parábola possui um ponto em comum com o eixo x.
• ∆ > 0: possui duas raízes reais, a parábola possui dois pontos em comum com o eixo x.

Vértices de uma parábola
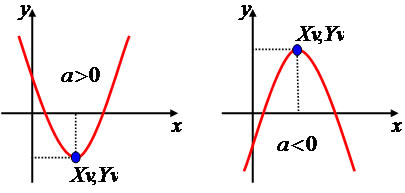
A parábola possui alguns pontos importantes na sua análise. Se a função possui a > 0 a parábola possui um ponto determinado mínimo e se a < 0, a parábola possui um ponto máximo.

Coordenadas do vértice de uma parábola