Embora não seja estritamente necessário, a resolução desta questão também se
utiliza de diagramas de flechas para que você tenha uma visão gráfica do
conteúdo explanado.
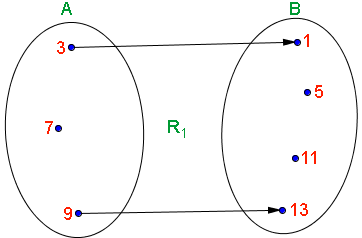 Pela definição de função sabemos que uma relação de A em B é função quando todos os
elementos do conjunto A estão relacionados a um, e
somente um, elemento do conjunto B.
Pela definição de função sabemos que uma relação de A em B é função quando todos os
elementos do conjunto A estão relacionados a um, e
somente um, elemento do conjunto B.
Segundo tal definição a relação R1 não é função, pois não existe nenhum par ordenado que relacione o elemento 7 do conjunto A, a qualquer elemento do conjunto B.
Em nenhum dos pares ordenados da relação R1 o primeiro elemento do par ordenado é o número 7 do conjunto A.
Observe no diagrama de flechas desta relação, que do elemento 7 do conjunto A não parte nenhuma flecha.
Então, segundo da definição de função, a relação R1 não é função.
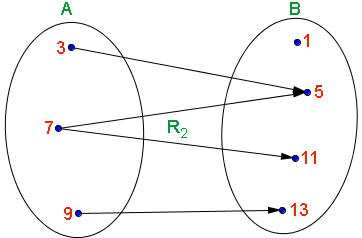 Na relação R2, para todo elemento do
conjunto A há ao menos um par ordenado que relaciona um
elemento de A a um elemento de B.
Na relação R2, para todo elemento do
conjunto A há ao menos um par ordenado que relaciona um
elemento de A a um elemento de B.
O problema neste caso é que o elemento 7 do conjunto A esta relacionado a mais de um elemento do conjunto B, através dos pares ordenados (7, 5) e (7, 11).
Note no diagrama de flechas da relação R2, que do elemento 7 do conjunto A partem duas flechas em direção ao conjunto de chegada, relacionando-o com os elementos 5 e 11 do conjunto B.
Então, segundo da definição de função, a relação R2 também não é função.
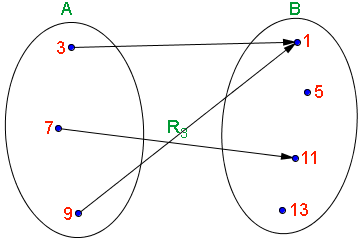 A R3 relaciona cada elemento do conjunto
A a um, e somente um, elemento do conjunto B.
A R3 relaciona cada elemento do conjunto
A a um, e somente um, elemento do conjunto B.
Veja que nem todos os elementos de B recebem flechadas de algum elemento de A, mas isto não contraria a definição de função.
Os elementos 5 e 13 pertencem ao contradomínio da função, mas não pertencem ao seu conjunto imagem.
Observe também que o elemento 1 do conjunto B recebe mais de uma flechada, não contrariando contudo, a definição de função.
Portanto, a relação R3 é função.
 As relações
R1 e R2 não se tratam de funções de A em B.
As relações
R1 e R2 não se tratam de funções de A em B.
 Pela definição de função sabemos que uma relação de A em B é função quando todos os
elementos do conjunto A estão relacionados a um, e
somente um, elemento do conjunto B.
Pela definição de função sabemos que uma relação de A em B é função quando todos os
elementos do conjunto A estão relacionados a um, e
somente um, elemento do conjunto B.Segundo tal definição a relação R1 não é função, pois não existe nenhum par ordenado que relacione o elemento 7 do conjunto A, a qualquer elemento do conjunto B.
Em nenhum dos pares ordenados da relação R1 o primeiro elemento do par ordenado é o número 7 do conjunto A.
Observe no diagrama de flechas desta relação, que do elemento 7 do conjunto A não parte nenhuma flecha.
Então, segundo da definição de função, a relação R1 não é função.
 Na relação R2, para todo elemento do
conjunto A há ao menos um par ordenado que relaciona um
elemento de A a um elemento de B.
Na relação R2, para todo elemento do
conjunto A há ao menos um par ordenado que relaciona um
elemento de A a um elemento de B.O problema neste caso é que o elemento 7 do conjunto A esta relacionado a mais de um elemento do conjunto B, através dos pares ordenados (7, 5) e (7, 11).
Note no diagrama de flechas da relação R2, que do elemento 7 do conjunto A partem duas flechas em direção ao conjunto de chegada, relacionando-o com os elementos 5 e 11 do conjunto B.
Então, segundo da definição de função, a relação R2 também não é função.
 A R3 relaciona cada elemento do conjunto
A a um, e somente um, elemento do conjunto B.
A R3 relaciona cada elemento do conjunto
A a um, e somente um, elemento do conjunto B.Veja que nem todos os elementos de B recebem flechadas de algum elemento de A, mas isto não contraria a definição de função.
Os elementos 5 e 13 pertencem ao contradomínio da função, mas não pertencem ao seu conjunto imagem.
Observe também que o elemento 1 do conjunto B recebe mais de uma flechada, não contrariando contudo, a definição de função.
Portanto, a relação R3 é função.
 As relações
R1 e R2 não se tratam de funções de A em B.
As relações
R1 e R2 não se tratam de funções de A em B.
Uma função para ser bijetora deve ser simultaneamente
sobrejetora e injetora.
Uma função é sobrejetora quando não há no contradomínio qualquer elemento que não esteja relacionado a nenhum elemento do domínio, ou em outras palavras, em uma função sobrejetora o conjunto imagem é o próprio contradomínio, visto que todos os elementos do conjunto de chegada recebem ao menos uma flechada.
Uma função é injetora quando cada elemento do conjunto imagem está relacionado a somente um elemento do conjunto de partida, ou seja, cada elemento do conjunto imagem recebe exatamente uma flechada.
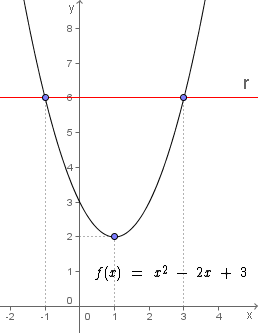 Como sabemos, f(x) = x2 - 2x + 3 é uma função polinomial do segundo grau, não sendo
portanto, uma função injetora, pois sendo o seu gráfico
uma parábola, se traçarmos uma reta paralela ao eixo das abscissas que corte a parábola em algum
local que não seja o seu vértice, tal reta a interceptará em dois pontos com a
mesma imagem.
Como sabemos, f(x) = x2 - 2x + 3 é uma função polinomial do segundo grau, não sendo
portanto, uma função injetora, pois sendo o seu gráfico
uma parábola, se traçarmos uma reta paralela ao eixo das abscissas que corte a parábola em algum
local que não seja o seu vértice, tal reta a interceptará em dois pontos com a
mesma imagem.
Observe a figura ao lado.
Note que a parábola é interceptada nos pontos (-1, 6) e (3, 6) pela reta r, paralela ao eixo x.
Veja que tanto para x = -1, quanto para x = 3, temos y = 6, ou seja, ambos os elementos do domínio possuem a mesma imagem 6.
Agora observe o vértice da parábola no ponto (1, 2), note que este é o ponto de mínimo desta função.
Perceba que para quaisquer valores de y < 2 não pertencem ao conjunto imagem da função, pois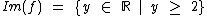
Como no caso desta função o conjunto imagem não é o próprio contradomínio, então esta função também não é sobrejetora, pois existem elementos no contradomínio que não estão relacionados a nenhum elemento do domínio, por exemplo, não existe qualquer valor real que atribuído ao x da função resulte em y = 1, já que o valor mínimo é y = 2.
 Não, a função
f(x) = x2 - 2x + 3 não é bijetora, pois não é nem injetora, nem
tampouco sobrejetora.
Não, a função
f(x) = x2 - 2x + 3 não é bijetora, pois não é nem injetora, nem
tampouco sobrejetora.
Uma função é sobrejetora quando não há no contradomínio qualquer elemento que não esteja relacionado a nenhum elemento do domínio, ou em outras palavras, em uma função sobrejetora o conjunto imagem é o próprio contradomínio, visto que todos os elementos do conjunto de chegada recebem ao menos uma flechada.
Uma função é injetora quando cada elemento do conjunto imagem está relacionado a somente um elemento do conjunto de partida, ou seja, cada elemento do conjunto imagem recebe exatamente uma flechada.
 Como sabemos, f(x) = x2 - 2x + 3 é uma função polinomial do segundo grau, não sendo
portanto, uma função injetora, pois sendo o seu gráfico
uma parábola, se traçarmos uma reta paralela ao eixo das abscissas que corte a parábola em algum
local que não seja o seu vértice, tal reta a interceptará em dois pontos com a
mesma imagem.
Como sabemos, f(x) = x2 - 2x + 3 é uma função polinomial do segundo grau, não sendo
portanto, uma função injetora, pois sendo o seu gráfico
uma parábola, se traçarmos uma reta paralela ao eixo das abscissas que corte a parábola em algum
local que não seja o seu vértice, tal reta a interceptará em dois pontos com a
mesma imagem.Observe a figura ao lado.
Note que a parábola é interceptada nos pontos (-1, 6) e (3, 6) pela reta r, paralela ao eixo x.
Veja que tanto para x = -1, quanto para x = 3, temos y = 6, ou seja, ambos os elementos do domínio possuem a mesma imagem 6.
Agora observe o vértice da parábola no ponto (1, 2), note que este é o ponto de mínimo desta função.
Perceba que para quaisquer valores de y < 2 não pertencem ao conjunto imagem da função, pois
Como no caso desta função o conjunto imagem não é o próprio contradomínio, então esta função também não é sobrejetora, pois existem elementos no contradomínio que não estão relacionados a nenhum elemento do domínio, por exemplo, não existe qualquer valor real que atribuído ao x da função resulte em y = 1, já que o valor mínimo é y = 2.
 Não, a função
f(x) = x2 - 2x + 3 não é bijetora, pois não é nem injetora, nem
tampouco sobrejetora.
Não, a função
f(x) = x2 - 2x + 3 não é bijetora, pois não é nem injetora, nem
tampouco sobrejetora.
Em caso de omissão do domínio e do contradomínio, assumimos que o contradomínio é o conjunto dos números
reais, 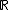 . Já em relação ao
domínio precisamos levar em conta outras
considerações.
. Já em relação ao
domínio precisamos levar em conta outras
considerações.
No caso desta função temos um radical no numerador da fração.
Como sabemos, o radicando real de um radical de índice par não pode ser negativo, de onde concluímos em relação ao numerador que:
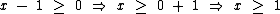
Também sabemos que o logaritmando de um logaritmo em qualquer base deve ser maior que zero, o que nos leva a esta outra consideração em relação ao denominador:
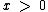
Não podemos nos esquecer que o logaritmo decimal de 1 é igual a 0, então x não pode ser igual a 1, caso contrário teremos um denominador igual a 0 e sabemos que não podemos realizar a divisão por zero no conjunto dos números reais, portanto temos uma terceira condição que é:
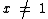
Vamos tomar como exemplo x = 1/2. Veja que este valor satisfaz a segunda condição, pois 1/2 é maior que 0, e também a terceira já que 1/2 é diferente de 1, no entanto não satisfaz a primeira condição, visto que x deve ser maior ou igual a 1 e não é.
Como as três condições precisam ser satisfeitas, a condição adotada será x > 1, já que quando x > 1, certamente será maior que 0 e diferente de 1, além de satisfazer a primeira condição.
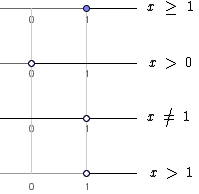 Ao lado temos a representação gráfica da explicação acima.
Ao lado temos a representação gráfica da explicação acima.
Na primeira linha temos a condição x ≥ 1.
Na segunda linha temos a condição x > 0.
Na terceira linha temos a condição x ≠ 1.
Na quarta linha temos a condição que satisfaz todas as três condições simultaneamente.
Em função disto o domínio desta função é:
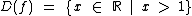
E a função pode ser assim definida:
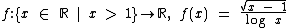

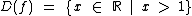 e
e 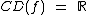 .
.
No caso desta função temos um radical no numerador da fração.
Como sabemos, o radicando real de um radical de índice par não pode ser negativo, de onde concluímos em relação ao numerador que:
Também sabemos que o logaritmando de um logaritmo em qualquer base deve ser maior que zero, o que nos leva a esta outra consideração em relação ao denominador:
Não podemos nos esquecer que o logaritmo decimal de 1 é igual a 0, então x não pode ser igual a 1, caso contrário teremos um denominador igual a 0 e sabemos que não podemos realizar a divisão por zero no conjunto dos números reais, portanto temos uma terceira condição que é:
Vamos tomar como exemplo x = 1/2. Veja que este valor satisfaz a segunda condição, pois 1/2 é maior que 0, e também a terceira já que 1/2 é diferente de 1, no entanto não satisfaz a primeira condição, visto que x deve ser maior ou igual a 1 e não é.
Como as três condições precisam ser satisfeitas, a condição adotada será x > 1, já que quando x > 1, certamente será maior que 0 e diferente de 1, além de satisfazer a primeira condição.
 Ao lado temos a representação gráfica da explicação acima.
Ao lado temos a representação gráfica da explicação acima.Na primeira linha temos a condição x ≥ 1.
Na segunda linha temos a condição x > 0.
Na terceira linha temos a condição x ≠ 1.
Na quarta linha temos a condição que satisfaz todas as três condições simultaneamente.
Em função disto o domínio desta função é:
E a função pode ser assim definida:

O que temos de fazer neste problema é encontrarmos a função inversa de 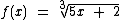 .
.
Para simplificar o desenvolvimento vamos substituir f(x) por y:
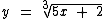
Agora invertemos a posição das variáveis x e y:
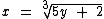
O próximo passo é isolarmos a variável y no primeiro membro:
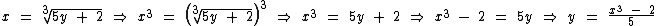
 Como y é igual a f(x), a
função inversa y-1 será:
Como y é igual a f(x), a
função inversa y-1 será:
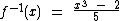
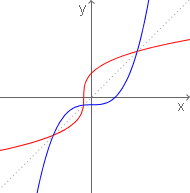
Veja que o gráfico de f(x), em vermelho, é simétrico ao gráfico de f-1(x), em azul, em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Esta é uma característica do gráfico de uma função com o da sua função inversa.
Funções como esta, que possuem uma função inversa, as denominamos funções inversíveis.
Lembre-se que para ser uma função inversível, ela precisa ser bijetora.
 f-1
é definida como
f-1
é definida como 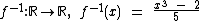 .
.
Para simplificar o desenvolvimento vamos substituir f(x) por y:
Agora invertemos a posição das variáveis x e y:
O próximo passo é isolarmos a variável y no primeiro membro:
 Como y é igual a f(x), a
função inversa y-1 será:
Como y é igual a f(x), a
função inversa y-1 será:Veja que o gráfico de f(x), em vermelho, é simétrico ao gráfico de f-1(x), em azul, em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Esta é uma característica do gráfico de uma função com o da sua função inversa.
Funções como esta, que possuem uma função inversa, as denominamos funções inversíveis.
Lembre-se que para ser uma função inversível, ela precisa ser bijetora.
 f-1
é definida como
f-1
é definida como
Como não foi informado, o contradomínio da função é
o próprio conjunto dos números
reais.
Já que não há qualquer restrição, visto que todo número real possui um quadrado, então o domínio da função também é o próprio conjunto dos números reais.
Então a definição desta função é:
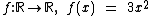
Para obtermos a definição da função inversa vamos substituir f(x) por y e depois isolá-la no primeiro membro:
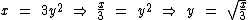
Então teríamos a seguinte função inversa:
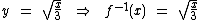
Falta ainda definirmos o domínio e o contradomínio desta função inversa.
Para isto devemos nos lembrar que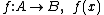 implica em
implica em 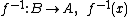 .
Traduzindo, significa dizer que o domínio da função é o contradomínio da sua
inversa e o contradomínio da função é o domínio da sua inversa.
.
Traduzindo, significa dizer que o domínio da função é o contradomínio da sua
inversa e o contradomínio da função é o domínio da sua inversa.
Em função disto a definição da função inversa seria:
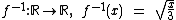
Você consegue identificar alguma coisa errada nesta definição?
Em outras palavras, ela diz que para todo número real x, existe um outro número real f-1(x), obtido a partir da lei de formação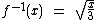 , mas
sabemos que isto não é verdade. Por quê?
, mas
sabemos que isto não é verdade. Por quê?
Simplesmente porque não existe raiz quadrada real de um número real negativo.
Então, corrigindo, a definição da função seria:
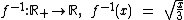
Observe que o domínio de f-1(x) não é o contradomínio f(x).
Isto quer dizer o quê?
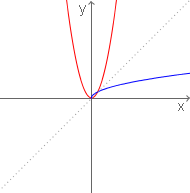 Quer dizer que a função f-1(x) não é
verdadeiramente a função inversa da f(x), pois f-1(x) não está definida para qualquer x menor que zero. Veja que o gráfico de f-1(x), em azul, não ultrapassa o eixo x.
Quer dizer que a função f-1(x) não é
verdadeiramente a função inversa da f(x), pois f-1(x) não está definida para qualquer x menor que zero. Veja que o gráfico de f-1(x), em azul, não ultrapassa o eixo x.
Observe que o gráfico de f(x), em vermelho, não é simétrico ao gráfico de f-1(x) em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Isto demonstra graficamente que estas funções não são uma o inverso da outra.
Não existe a função inversa de f(x), pois ela não é bijetora. As funções quadráticas não o são.
Isto já basta para resolver o problema. Ao invés de tão prolixo, este artigo poderia ser bem conciso, no entanto foi redigido desta forma para lhe passar mais alguns conceitos importantes.
Veja também que f-1(x) não é uma função sobrejetora e consequentemente não é bijetora.
Se você não se recorda do que se tratam estes tipos de função, esta é uma boa oportunidade para fazer uma recapitulação
 A função
3x2 não é inversível, pois não é bijetora e, portanto, não possui uma
função inversa.
A função
3x2 não é inversível, pois não é bijetora e, portanto, não possui uma
função inversa.
Já que não há qualquer restrição, visto que todo número real possui um quadrado, então o domínio da função também é o próprio conjunto dos números reais.
Então a definição desta função é:
Para obtermos a definição da função inversa vamos substituir f(x) por y e depois isolá-la no primeiro membro:
Então teríamos a seguinte função inversa:
Falta ainda definirmos o domínio e o contradomínio desta função inversa.
Para isto devemos nos lembrar que
Em função disto a definição da função inversa seria:
Você consegue identificar alguma coisa errada nesta definição?
Em outras palavras, ela diz que para todo número real x, existe um outro número real f-1(x), obtido a partir da lei de formação
Simplesmente porque não existe raiz quadrada real de um número real negativo.
Então, corrigindo, a definição da função seria:
Observe que o domínio de f-1(x) não é o contradomínio f(x).
Isto quer dizer o quê?
 Quer dizer que a função f-1(x) não é
verdadeiramente a função inversa da f(x), pois f-1(x) não está definida para qualquer x menor que zero. Veja que o gráfico de f-1(x), em azul, não ultrapassa o eixo x.
Quer dizer que a função f-1(x) não é
verdadeiramente a função inversa da f(x), pois f-1(x) não está definida para qualquer x menor que zero. Veja que o gráfico de f-1(x), em azul, não ultrapassa o eixo x.Observe que o gráfico de f(x), em vermelho, não é simétrico ao gráfico de f-1(x) em relação à bissetriz dos quadrantes ímpares do plano cartesiano. Isto demonstra graficamente que estas funções não são uma o inverso da outra.
Não existe a função inversa de f(x), pois ela não é bijetora. As funções quadráticas não o são.
Isto já basta para resolver o problema. Ao invés de tão prolixo, este artigo poderia ser bem conciso, no entanto foi redigido desta forma para lhe passar mais alguns conceitos importantes.
Veja também que f-1(x) não é uma função sobrejetora e consequentemente não é bijetora.
Se você não se recorda do que se tratam estes tipos de função, esta é uma boa oportunidade para fazer uma recapitulação
 A função
3x2 não é inversível, pois não é bijetora e, portanto, não possui uma
função inversa.
A função
3x2 não é inversível, pois não é bijetora e, portanto, não possui uma
função inversa.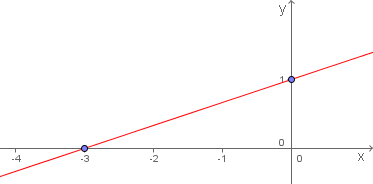 Funções afim são representadas graficamente por uma
reta não paralela ao eixo x.
Funções afim são representadas graficamente por uma
reta não paralela ao eixo x.Ao lado temos o gráfico da função afim que passa pelos referidos pontos, os quais também pertencem aos eixos do plano cartesiano.
O ponto (-3, 0) é comum à reta e ao eixo das abscissas.
O ponto (0, 1) é comum à função e ao eixo das ordenadas.
A lei de formação de uma função afim é da forma
Podemos identificar o valor numérico dos coeficientes a e b, substituindo os valores de x e y dos referidos pontos.
Para o ponto (0, 1) temos:
Agora que sabemos que b = 1, para o ponto (-3, 0) temos:
Conhecendo a e b já temos condição de obter a lei de formação da função:
Assim a função
 A lei de
formação desta função é
A lei de
formação desta função é
Uma função linear é da forma 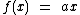 com
com 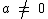 , ou seja, é
uma função afim da forma
, ou seja, é
uma função afim da forma 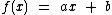 , com
, com 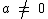 e com
e com 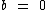 .
.
 Segundo o enunciado, um determinado ponto desta função linear é identificado
por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa
x.
Segundo o enunciado, um determinado ponto desta função linear é identificado
por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa
x.
O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a
função linear com tais características seja uma função afim, ela é uma função
decrescente.
Não, embora a
função linear com tais características seja uma função afim, ela é uma função
decrescente.
 Segundo o enunciado, um determinado ponto desta função linear é identificado
por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa
x.
Segundo o enunciado, um determinado ponto desta função linear é identificado
por (x, -x), isto é, o valor da ordenada y é o oposto do valor da abscissa
x.O seu gráfico temos ao lado.
Para obtê-lo escolhemos dois pontos aleatoriamente, segundo a indicação do enunciado e traçamos a reta que os contém.
Obviamente este é o gráfico de uma função decrescente e não de uma função crescente.
Mas você não precisa ter o gráfico para solucionar este problema.
Já que os pontos do gráfico são (x, -x), quando aumentamos o valor de x, consequentemente diminuímos o valor de y que é igual a -x, então tal função é decrescente, pois para ser crescente, ao aumentarmos o valor de x, o valor de y também deveria aumentar.
 Não, embora a
função linear com tais características seja uma função afim, ela é uma função
decrescente.
Não, embora a
função linear com tais características seja uma função afim, ela é uma função
decrescente.
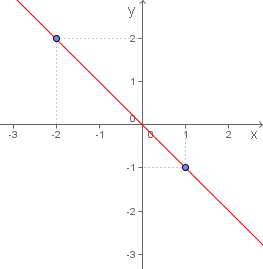
Dizer que f(7) = 78 é a mesma coisa que dizer que o
gráfico desta função afim passa pelo ponto (7, 78).
Então este problema requer na verdade que se obtenha a lei de formação da função afim que passa pelos pontos (3, 22) e (7, 78) e que a partir dela calculemos a ordenada do ponto desta função, cuja abscissa é igual a 12.
Já temos no site exemplos de problemas onde damos dois pontos de uma função afim e solicitamos que seja obtida a regra de associação da função. Para variar um pouco, agora vamos solucionar este problema através da resolução de um sistema de equação do primeiro grau com duas incógnitas pelo método da adição.
Visto que a lei de formação de uma função afim é da forma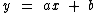 , a partir dos pontos
conhecidos podemos equacionar o seguinte sistema:
, a partir dos pontos
conhecidos podemos equacionar o seguinte sistema:
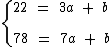
Note que para cada ponto temos uma equação obtida da lei de formação, na qual x e y foram substituídos pelo respectivo elemento do par ordenado do ponto em questão. A primeira linha se refere ao ponto (3, 22) e a segunda ao ponto (7, 78).
Para solucionar o sistema vamos começar multiplicando a primeira equação por -1:
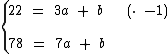
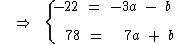
Agora podemos somá-las para que o valor de a seja obtido:
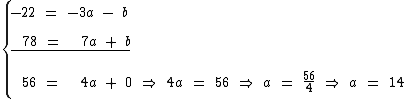
O valor de b vamos obter substituindo a por 14 na primeira equação:
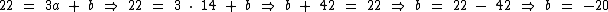
Sendo a = 14 e b = -20 temos a seguinte regra de associação:
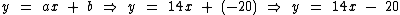
Então só nos resta calcular a ordenada do ponto desta função cujo valor da abscissa é igual a 12, que nada mais é que f(12):
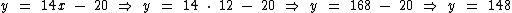
 A ordenada do
ponto desta função cujo valor da abscissa é igual a 12 é 148.
A ordenada do
ponto desta função cujo valor da abscissa é igual a 12 é 148.
Então este problema requer na verdade que se obtenha a lei de formação da função afim que passa pelos pontos (3, 22) e (7, 78) e que a partir dela calculemos a ordenada do ponto desta função, cuja abscissa é igual a 12.
Já temos no site exemplos de problemas onde damos dois pontos de uma função afim e solicitamos que seja obtida a regra de associação da função. Para variar um pouco, agora vamos solucionar este problema através da resolução de um sistema de equação do primeiro grau com duas incógnitas pelo método da adição.
Visto que a lei de formação de uma função afim é da forma
Note que para cada ponto temos uma equação obtida da lei de formação, na qual x e y foram substituídos pelo respectivo elemento do par ordenado do ponto em questão. A primeira linha se refere ao ponto (3, 22) e a segunda ao ponto (7, 78).
Para solucionar o sistema vamos começar multiplicando a primeira equação por -1:
Agora podemos somá-las para que o valor de a seja obtido:
O valor de b vamos obter substituindo a por 14 na primeira equação:
Sendo a = 14 e b = -20 temos a seguinte regra de associação:
Então só nos resta calcular a ordenada do ponto desta função cujo valor da abscissa é igual a 12, que nada mais é que f(12):
 A ordenada do
ponto desta função cujo valor da abscissa é igual a 12 é 148.
A ordenada do
ponto desta função cujo valor da abscissa é igual a 12 é 148.
Ao estudarmos as relações
entre coeficientes e raízes das equações do segundo grau vimos as seguintes
relações:
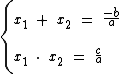
Como no ponto (3, 0) a função apenas tangencia o eixo das abscissas, isto significa que tal função possui duas raízes reais e iguais a 3.
No caso as raízes são a abscissa deste ponto, ou seja, ambas as raízes são iguais a 3.
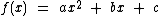 é a lei de formação de uma função quadrática
é a lei de formação de uma função quadrática  , com
, com 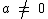 (
(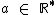 ,
, 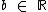 e
e 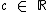 .
.
O fato de a função interceptar o eixo das ordenadas no ponto (0, -9), nos indica que o valor do coeficiente c é -9, pois a parábola do gráfico de uma função polinomial do segundo grau sempre intercepta o eixo y no ponto (0, c).
Sabendo-se que c =-9 e que x1 = x2 = 3, a partir da segunda relação acima temos:
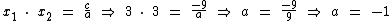
Agora sabemos que c =-9, x1 = x2 = 3 e que a =-1. Então, a partir da primeira relação supracitada:
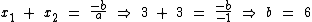
Os coeficientes da função quadrática são então:
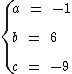
Que nos leva à seguinte definição de função:
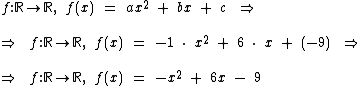
 A definição
desta função é:
A definição
desta função é: 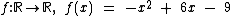 .
.
Como no ponto (3, 0) a função apenas tangencia o eixo das abscissas, isto significa que tal função possui duas raízes reais e iguais a 3.
No caso as raízes são a abscissa deste ponto, ou seja, ambas as raízes são iguais a 3.
O fato de a função interceptar o eixo das ordenadas no ponto (0, -9), nos indica que o valor do coeficiente c é -9, pois a parábola do gráfico de uma função polinomial do segundo grau sempre intercepta o eixo y no ponto (0, c).
Sabendo-se que c =-9 e que x1 = x2 = 3, a partir da segunda relação acima temos:
Agora sabemos que c =-9, x1 = x2 = 3 e que a =-1. Então, a partir da primeira relação supracitada:
Os coeficientes da função quadrática são então:
Que nos leva à seguinte definição de função:
 A definição
desta função é:
A definição
desta função é: